The Pitch-Drop Experiment and the Tyranny of Temperature in Science Education

Our natural understanding of matter is very self-centered. When ascribing properties to substances, we are quite subjective in our conclusions. We say rubber is elastic because it exhibits elasticity under the conditions we typically see. We think of ice as a solid because we are far more used to encountering it inside our freezers than on a flowing glacier. Furthermore, our perception of time biases us from seeing the motion of a glacier in the same light as the flowing of, say, honey.

It is natural for science to attempt to codify and explain these natural categorizations. Schoolchildren are treated to a relentless drumming of the basic “definition” of a solid as something that has a definite shape and does not flow. Similarly, students are told that liquids flow and have no definite shape but do have a definite volume while gases have neither definite shape nor volume.

Are Solids so Simple? Some Elementary Objections

On their own, these efforts at codifying the states of matter are reasonably accurate if you are speaking of practical experience, but science aspires to more precision and objectivity than this. Science attempts to describe how the world works in a non-self-absorbed way, and in this sense even these heuristics are rather lacking. In particular, solids do not have a definite shape. A piece of paper is a solid material, but you can fold it and it gets a new shape. In fact, I don’t even have to bend it; allow a sheet of paper to drape over the edge of the desk and it will have a different shape than it did when it was lying flat. As to whether solids “flow” or not, that depends on how you define the term. What makes the deformation of a stretched bungee cord any different than the deformation of honey poured from a bottle?

To address these examples, a science teacher who wants to toe the party line has to act much like the spokesman for a politician with a penchant for impolitic remarks. Each separate example gets its own excuse and explanation, but those explanations do not have a consistent message:

Reporter 1: Why did Mr. Textbook say that a solid has a definite shape when you can bend a piece of paper?

Spokesman: Mr. Textbook wasn’t referring to all types of forces acting on a solid; just gravity.

Reporter 2: What about the bungee cord?

Spokesman: What Mr. Textbook meant was that a solid doesn’t change shape based on its own weight.

Reporter 3: What about the paper draped over the edge?

Spokesman: Mr. Textbook wasn’t talking about temporary changes. He just meant that a solid will go back to its shape once the force is removed.

And at this point Reporter 1 and Reporter 3 stare at each other in disbelief.


A More Accurate Mantra, and More Significant Issues

The objections raised in the previous section are, in some sense, elementary. They are mostly semantic in nature, but I believe they are still relevant. If we are going to have students accept a mantra (“A solid is …”) and repeat it over and over every grade, we should at least get the mantra right or be clear what we mean.

A more accurate way of conveying what textbooks mean would be to say something like “Solids don’t drip.” It avoids the red herring of “definite shape” and focuses on the notion of “flow” while combining with it the idea of non-elasticity. A bungee cord is critically different from honey in that a bungee cord, once it snaps, will return to its original shape. A drop of honey, after it falls, will remain a drop, not returning to whatever shape the honey had before it was poured. We say that liquids are viscous while solids are elastic because of this difference.

Using the clause “solids don’t drip” to differentiate between liquids and solids gets around the elementary problems with the textbook definitions of solid, liquid, and gas, but it cannot cope with a more severe problem. In essence, science education has painted itself into a corner by trying so hard to link states of matter with temperature.

Readers of Science Myths Unmasked Volume 2 will know that most of what is learned in school about temperature and phase change is wrong. Solids do not change to liquids at the “melting point.” Liquids do not boil at the “boiling point,” and temperature does not determine phase. The story told in textbooks is a fairy tale designed to help students remember certain facts at the expense of understanding what is going on.
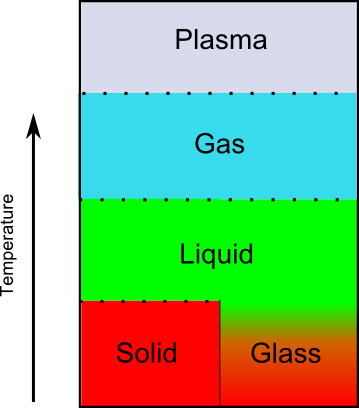
When it comes to teaching about states of matter, the interest in pinning so much on temperature actually distorts the entire picture given to students from the beginning. The textbook presentation is committed to a story where there are clear breaks between phases, occurring at set temperatures, and this puts kids on the wrong path from the beginning. The textbook regime only works for crystal solids, like iron, ice, and diamond. It doesn’t work for amorphous materials like wood, glass, and rubber. Since the textbook narrative only works for crystal solids, those are the examples students are shown. When discussing phases and phase changes, students are regularly provided illustrations of solids as comprising small molecules packed into well-defined lattices. The explanations of melting and other physical properties associated with solids tend to reinforce this incomplete picture.

A more accurate depiction of states of matter would make a clear distinction between crystal solids and amorphous materials that are designated as glasses by scientists. These are objects that seem solid but do not have a regular crystal structure. (Not all amorphous solids are glasses, but the exceptions are mostly materials that do not undergo typical phase changes. A simple example is wood. We don’t speak of wood “melting” because it undergoes chemical reactions well before the physical reaction of deliquescence. )

There are two reasons why the above picture would upend textbook orthodoxy, and both have to do with the outsize role given to temperature. First, this diagram suggests (quite rightly) that temperature does not determine phase. A substance can start out as a solid, be heated into a liquid, and then (upon cooling) become a glass, moving from the region marked “Solid” in the diagram, around the vertical, solid line, to wind up (at the same temperature) in the “Glass” region. If you take liquid water and cool it in one way, you get solid ice, like the cubes in your freezer. If you take that same liquid water and cool it in a different way, you get a different substance called glassy water. The transitions that substances make depend on more than temperature. (Note that there are several other reasons why temperature doesn’t determine phase. Those are not captured by this diagram but are discussed in Science Myths Unmasked Volume 2.)

The second reason this diagram would be heretical in standard science education is that textbooks want to hammer into students’ skulls the idea that changes in state occur at particular temperatures. In the above illustration, we see that the glass state transitions to the liquid state gradually. In fact, the “glass” state is not even considered a separate phase from the liquid in the normal sense of the word “phase.” (There are properties liquids have that objects in glass form do not have, but they are very different from the properties used to differentiate (crystal) solids from liquids.)

In many ways, “glasses” are better seen scientifically as very slow-flowing liquids than as solids, but we humans (being very self-absorbed in our labeling) tend to think of them more as solids than liquids because they react like solids in most day-to-day encounters.

An excellent demonstration showing how amorphous solids are like liquids is the “Pitch Drop Experiment,” which you can read about and see live here . This demonstration shows the fluid properties of pitch, a rubbery substance used to waterproof boats. It takes about 9 years for a drop to form. In our day-to-day experience, pitch acts like a solid, but on a longer timescale, it acts like a liquid.

Notably, this notion that glasses can be seen as simply “slow-flowing” liquids has more depth to it than you might think. A key notion separating liquids from solids is that solids often return to their original shape after being deformed while liquids do not. However, the response of a material to a deformation heavily depends on how rapidly the deformation occurs. A material can act like a solid at 20 degrees C when it is deformed at a certain rate but act like a liquid at the same temperature when deformed at a different rate.

This principle, called Time-Temperature Superposition, has real application in materials science. A scientist can measure the elastic properties at one temperature at a particular rate of deformation and predict how the same material will act at a different temperature at a different rate of deformation.

Of course, I cannot help but point out that this gives yet another example of how temperature does not, by itself, determine changes in the properties of matter.

(Note: A careful reader might wonder about the flowing of ice in glaciers given that ice is a crystal substance. The dynamics causing ice to flow in a glacier are fundamentally different from the flow seen in the pitch-drop experiment. It is not clear whether a small sample of ice would ever flow in this way if it were kept in conditions preventing liquefaction. Still, the example is good to bear in mind when considering the absolute statements made in textbooks, and we could make a claim that describing a liquid as something that “flows” is itself a fundamental error.)

Electrons are not so elementary

An interesting article at popsci claims that electrons have now been “seen” splitting into quasi particles.

Where is the Sun? (Addendum)

At the end of my second post on the position of the sun, I suggested as a challenge question determining the direction of sunrise or sunset on a solstice at the equator. I’m giving an illustration here showing the answer.

As is the case for many mathematical questions, visualization is key. We are very used to depictions of the sun and Earth where the latter is tilted on its axis. It is easier to consider the problem if we un-tilt our bearing and picture Earth’s axis as straight up-and-down with Earth rotating left-to-right (for points on the “front” side). Un-tilting Earth essentially means rotating our view.

Note that the image shown above is nothing more than the picture given in my first post on the position of the sun, but rotated 23.4 degrees. For the person at the blue dot, The sun is setting, she is about to be rotated into the dark area. Points to the north still have some daylight left, and the farther north you go, the longer the day is.

I think it is pretty clear from the picture that the sun is situated 23.4 degrees north of due west. For sunrise, the same type of picture could be drawn, but we would want Earth on the left-hand side of the drawing. Note that the same drawing would not work on other days. On the solstice, Earth’s tilt points directly at the sun, so this simple rotation is easy to visualize.

Where is the Sun: Part II

In the earlier post on this topic, I wrote about the common myth that the sun is directly overhead at noon. Here, we’ll take a look at the even more common belief that the sun rises in the east and sets in the west.

You can generally answer almost any simple question about the position of the sun in the sky if you keep in mind three basic rules:

  • On each equinox the sun rises (nearly) due east and sets (nearly) due west. Its position near noon is determined by the latitude. On these days the sun should be directly overhead if you are on the equator (0 degrees latitude). If you are not on the equator than your latitude tells you how much you have to change the angle of your sight to look directly at the sun. For example, if you are at 20 degrees north latitude, then you will have to tilt your head 20 degrees (from “straight up” position) to the south. If you are at 50 degrees south latitude, you will need to tilt your head that many degrees to the north.
  • Because Earth is tilted approx. 23 and a half degrees, the position of the sun near noon will move by this amount (north or south) throughout the year. If you are at 30 degrees north latitude (near Austin, Texas), then the sun will appear only 30-23.4 = 6.6 degrees south of “straight up” in the heart of summer, generating Texas’ legendary heat. However, in the dead of winter, the sun will be 30+23.4=53.4 degrees south of “straight up,” leading to a mild environment.
  • For those in the northern hemisphere, the sun moves south after it rises until around noon. Then it moves northward until it sets. (This is in addition to its prevailing, general westward motion.)

I wrote about the first two points in the previous post on this topic. The third point generalizes one of the observations made in the first point. If the sun rises due east and is due south around noon, then it must have traveled southward during the morning. Similarly, if it is due south around noon and sets due west, it must have traveled northward in the PM hours. Most of the time, the sun does not rise due east or set due west, but it still follows the same pattern of moving southward until around noon and then moving back northward. In the southern hemisphere, the pattern is reversed. The sun moves northward from sunrise to noontime and the moves southward in the later hours.

Keeping the above notes in mind, let’s consider the question “To someone in Kansas, what direction is sunset around May 20?”

The spring equinox typically occurs around March 20th. We know that the sun rises due east on that day. By noon it appears to the south. Then it sets due west. The noontime sun in the summer is also in the south, but it is closer to being overhead. Instead of being, say 39 degrees south at noon, it might be only 19 degrees south in late May. The noontime position of the sun has moved northward around 20 degrees! (By the summer solstice it will have moved northward 23.4 degrees.)

In fact, the entire path of the sun has been shifted northward, meaning that the sun does not rise due east in summer but actually rises a little north of due east. Similarly, it does not set due west but rather a bit north. The noontime position of the sun has moved northward by 20 degrees, but the position of sunset has actually moved northward more. To understand why recall that the sun moves northward from noon until evening: sunset is now occurring at a later time, so the sun has more time to arc northward before it is swallowed by the horizon. Instead of being 20 degrees north of “due west,” the sun sets about 26 or 27 degrees north of due west, closer to NW than due west.

The effect for sunrise is the same: the sun rises about 26 or 27 degrees north of due east, so closer to NE than east.

The image below illustrates the narrative above. It depicts the path of the sun as seen from Golden Belt, KS. The orange arc shows the path traced out on March 20th. The sun rises nearly exactly due east (marked by the yellow line) and sets nearly exactly due west (shown by the reddish line). The orange line describes the direction to the sun’s image around 11 am.

From SunCalc.net

The orange region contains the possible paths of the sun on other days. The upper edge is the path the sun takes on the summer solstice: the sun rises east northeast and sets west northwest. The lower edge is the path in the middle of winter. Then it rises east southeast and sets west southwest. Below, I have inserted an image showing the path for today, August 5. The golden line segment running east northeast points in the direction of sunrise. The reddish line pointing west northwest points in the direction sunset. Here the orange bar describes the path to the sun around 1 pm.

From SunCalc.net

It turns out that, for most people in the US, the sun rises in the east about half the time, about a quarter of the time it rises closer to NE and about a quarter of the time it rises closer to SE. You can investigate the situation for your own location by using two nifty online tools. One is the sun position tool at sunearthtools.com. The other is suncalc.net, which I used to make the images above.

I should stress that for most points in the US the effect is mild. to illustrate this, think of a compass as a clock face, with north at 12 o’clock and south at 6 o’clock. For those living in the mid-latitudes of the U.S. (e.g., Kansas, Washington DC, Northern California), you can roughly say the sun rises at the 2 o’clock position in June and July, at 4 o’clock position in December and January, and at 3 o’clock (due east) in the months near the equinoxes (September, August, March, April).

For those living further north, the effect is more pronounced. For someone on the arctic circle, the sun rises in the north near the summer solstice!

One interesting mathematical challenge you may wish to pose to a precocious math student is “Where does the sun rise at the equator on a solstice?” It turns out to be 23.5 degrees (the same as the Earth’s tilt) north or south of due east (depending on which solstice). A corollary to this observation is that every person in the northern hemisphere sees the sun rise closer to NE than due east on that day.

Where is the Sun? — Part I (or Bad Science Flummoxes Vacations)

I took a mini-vacation to Brussels a couple of weeks ago, and having to navigate in a new location made me think of a common misconception held, I believe, by a large proportion of adults.

Most students are told that the sun reaches its highest point in the sky (its zenith) at noon. Now, this isn’t exactly true, but it is pretty close for most locations. However, that reasonably accurate principle is often abbreviated to the claim that the sun is directly overhead at noon, a belief many people retain their entire lives.

For the vast majority of Americans, the sun is nowhere near directly overhead at noon except in June and July, and this has several practical consequences.

Three dimensional geometry can be difficult to envision, but let’s look at a single, important case. On the summer solstice, Earth is tilted directly toward the sun. This is why the solstice is the longest day of the year. The angle of tilt is about 23.5 degrees, so someone at that northern latitude (23.5°) will see the sun nearly directly overhead at noon. This latitude is called the Tropic of Cancer. Below I have illustrated this statement and shown why someone standing north of this latitude will not see the sun directly overhead.

Since the entire continental United States lies above the Tropic of Cancer, no one in the extremely misnamed “lower 48” ever sees the sun directly overhead. (Those in Hawaii can.) For most of the year, the noon-time sun is quite far away from directly overhead in the US. For a student on spring break in Kansas City, KS, the inclination of the sun is about 51 degrees, not 90 degrees (which would correspond to the sun being directly overhead).

The above calculation assumes the student’s spring break is near the spring equinox (normally March 20), when it is easy to determine the inclination of the sun based on the latitude of the location. On an equinox Earth’s tilt is perpendicular to the path between Earth to the sun, so Earth’s tilt is irrelevant to the noon-time sun position. Someone standing on the equator (latitude = 0°) sees the sun directly overhead at noon, an inclination of 90 degrees. More generally, a latitude is L°, the inclination will be about 90 – L degrees at noon on an equinox.

Our hypothetical student will see the sun 39 degrees south of the center of her vision when she looks straight up. Because human field of vision is about +/- 50 degrees (vertically), the student in question is barely able to see the sun when looking straight up at noon. The image below gives some impression what the sky looks like to her. The size of the sun has been exaggerated.

Not only is it bad science to think the sun is overhead at noon (that could only occur on a flat, or at least cylindrical, Earth), but it can affect everyday life. For example, many people simply do not know how to tell direction by the position of the sun. This can be a useful tool, especially when vacationing in a new city. If you vacation in any location above the Tropic of Cancer, the sun is very close to directly south at noon. If you vacation to Australia, Argentina, or anywhere else below the Tropic of Capricorn, the sun will always be very close to directly north at noon. This basic information regarding the location of the noon-time sun is often enough to determine directions for most of the day, especially if you are in a city whose streets form a grid coordinated with the four cardinal directions.

This is part I of a two-part series on misconceptions regarding the course of the sun through the sky. In the second part we will discuss more complicated questions that cannot be explained using 2-dimensional geometry. For example, we will take a look at the common claim that the sun rises in the east and sets in the west.

Should We Apologize for Newton?

An aside buried in a recent post at Doyle’s science blog caught my eye. In discussing gravity with young students, he describes how one could talk about objects “pulling” on one another. He then, understandably, gives the disclaimer “Yes, of course, this is Newtonian and simplistic–we’re talking about 8 years olds.”

Now, on the one hand, I like it when people point out that we know that Newton’s views have been superseded. In fact, I would go further and say that it is very bad science to claim that Newton is “approximately” correct. Sure, in most cases one could pretend the universe acted as Sir Isaac conceived it and get an answer that is close to reality, but the same could be said of flat-earth astronomy and the fluid-theory of heat! Yet people would be appalled if we said that thinking about heat as a substance that flows from one object to another was “approximately” correct or that flat-earth astronomy was “approximately” correct. In point of fact, Einstein’s discovery of relatively showed that Newton’s entire conception of the universe, and in particular the notion that time and space were independent (which forms the heart of his method for doing physics) was utterly wrong.

Yet, these strong views about Newton aside, I also wonder if we show too much concern about giving the type of disclaimer Mr. Doyle does. I would say that the problem with statements like “objects exert a force on each other” does not lie in the statement itself, but rather in an over-rigid understanding of what “force” means. True, if you mix Newton’s definition of “force” with Einstein’s theory of relativity, you come to the conclusion that the statement is bad science, but the Newtonian definition of “force,” the version we feed to students in school, is in fact itself an artificial one, it has no basis in the natural world, so why do we hold it sacrosanct?

In fact, the scientists of the 19th century did not themselves conceive of a force in the way Newton did. Newton proposed the radical notion that there were specific “pushes” and “pulls” that could explain all changes in motion. His method of doing physics eventually became so compelling that all physicists saw phenomena in Newtonian terms. When that happened, scientists began seeing forces as “whatever causes a change in motion.” There was no requirement that these forces be understood or that they relate to a “push or pull” or anything else. Essentially, physicists had taken Newton’s view of the world as axiomatic so that any observed change in motion became tantamount to a “force.” Physicists had redefined the terms in such a way that Newton’s theory could not be disproved (almost). If they had maintained Newton’s actual views, any experiment where, say, magnetism or electrostatic repulsion affected the results would have disproved Newton’s theory, which had no way to account for repulsion at a distance.

(Incidentally, the reverse of this occurred in Chemistry with respect to Dalton’s Law of Multiple Proportions. Originally, Dalton defined a chemical reaction as one where his law held, meaning it could never be disproved. The fairy-tale given in chemistry textbooks about the history of this law does not respect the fact that at the time there was no clear way of discriminating between physical reactions (like dissolving) and chemical ones.)

In any event, this 19th century understanding, where “force” simply refers to whatever causes a change in motion, is no worse than the one we tell students, and it has the advantage of making statements like “every object exerts a force on every other object” true. It is genuinely true that the existence of an object at one point does influence what we humans perceive of the motion of another object. That is true in Einstein’s world as well as Newton’s. (It is just explained differently.)

Of course, we have to accept that this observation is hopelessly human-centric. The very idea of “change in motion,” which relies on a human conception of time as absolute and separate from space, is a modern-day equivalent to Ptolemaic astronomy. But Ptolemaic astronomy has its uses for our culture, and so does Newton’s perspective on motion, even if the Universe does not agree with it.

Perhaps just a step away from the Higgs

Physicists at CERN now say that are a “hair’s breadth” away from officially discovering the Higgs.

North Carolina gets the “Terrible Standard I Found Today” Award

I found a particularly bad science standard today in North Carolina:


3.P.3.1
Recognize that energy can be transferred from one object to another by rubbing them against each other.

Presumably this standard refers to friction. One cannot defend this standard by appealing to conduction for a variety of reasons (e.g., there is no mention of a difference in temperature, conduction is covered in another standard, and conduction has nothing to do with rubbing [except that rubbing would actually lessen the transfer of energy by creating a hump in the temperature profile]).

Friction should never be presented as a transfer of energy from one object to the object it is rubbed against. Conceiving of friction in this way leads to false conclusions. For example, imagine object A and object B are rubbed together. A transfers energy to B, meaning A loses energy and B gains it. B rubs against A, so B also loses energy and A gains it. If the objects are of identical composition, the only conclusion to be drawn is that the two exchanges cancel each other, causing no net change in temperature. This, of course, does not match what we see in nature.

At an abstract level, one could claim that rubbing A and B together permits and a transfer of energy FROM C, where C is whatever is causing the rubbing to occur. If a person is rubbing two blocks together, then energy is ultimately being transferred from the person’s stored energy reserves to the blocks.

At a more granular level, one should say that rubbing two objects together allows an energy transformation (not transfer) for each object individually. The coherent linear motion (the block’s molecules all moving together as a macroscopic entity) has a certain amount of linear kinetic energy associated to it. (It got this kinetic energy from C, the thing causing the rubbing.) The braking action of friction is really just the transformation of this linear kinetic energy into thermal energy (non-linear, microscopic, kinetic energy). But it is not a transfer of energy from one object to another, at least when viewed in a scenario as described in the standard, where both objects are seen as moving. (If you select a certain rest frame where one object is moving and the other is viewed as eternally fixed, one could make a claim that there is actual transfer but even this is very confusing for the student on many levels…not the least of which being that leads students to believe that the heat they feel when rubbing their hands together is evidence of energy transfer.)

In short, the heat felt when two objects are rubbed is evidence of energy transformation, one form of energy being changed to another form of energy. It is not evidence of energy transfer between objects.

Doyle skewers draft science standards

The amazing Mr. Doyle has a nice rundown of foibles in the current draft of the Next Generation Science Standards.

Chemistry Versus Physics: Why does “Heat Rise”? (Part 2 of 2)

Part 1 presented a basic conundrum: particles that are hotter (or lighter) than their peers tend to rise; for example steam will rise off boiling water to condense on a glass lid. The “explanation” given in physics textbooks makes no sense because the hotter (or lighter) particles are not bound together in a separate volume. One cannot treat hot steam rising in the same way as one treats the gas in a hot air balloon. The steam particles can freely intermix with their cooler peers and there is no surface for the cooler air to push up against to buoy the steam upwards.

Thus, the rising of hot (or light) particles appears to directly contradict basic principles students learn in chemistry and physics courses. They are taught the Kinetic Molecular Theory, which claims the behavior of a gas is determined by chaotic, random collisions among its particles. They are also taught that the downward acceleration of gravity for each particle is the same. So how can some particles be favored to move upward if gravity treats them all the same and the chaotic motion is random?
Here is the 3-sentence answer:

The collisions between particles are random but on average they tend to work against gravity. Lighter particles are affected more by collisions than heavier particles, and faster particles undergo more collisions than slower particles. Thus, lighter and faster particles gain more upward momentum than their (heavier or slower) peers.

Two notes regarding the above explanation bear discussion. The first is simple. Lighter particles are almost always moving faster than their heavier peers because temperature is a measure of kinetic energy, which depends on both mass and speed. Thus, if a gas is a mixture of two or more kinds of particles (in thermodynamic equilibrium) the lighter particle must be moving faster on average to make up for having less mass. Thus, lighter particles are often buoyed by both principles.

The second note is more involved. In my books I emphasize contradictions taught by science textbooks. For example, a chemistry textbook will state that temperature is a measure of the average kinetic energy possessed by the microscopic particles of a substance. The same book will later claim that particles in a gas move much faster than particles in a liquid. But how can these statements both be true if water and steam can exist at the same temperature and pressure? If they have the same temperature, their particles have the same average kinetic energy, and if their particles have the same average kinetic energy (and the same mass), how can the particles of steam be moving much faster than those of water?

Hence, when I give the 3-sentence answer above, I immediately hope a student will ask, “But how can collisions work to push particles upward if all collisions conserve momentum? In any given collision, whatever upward momentum one particle gains is lost by the other particle.”

It would be great if students were taught to have such skeptical, discriminating minds. Unfortunately, most students are conditioned to accept whatever is told to them, in science class no less!

Regarding this hypothetical student’s question, the first thing that must be noted is that if collisions produced no net lift, all the particles would be lying on one another on the floor, and we would not be having this conversation because there would be no oxygen to breathe. The second point is that not all collisions conserve momenta among the particles. Consider a single particle striking the floor and rebounding. It gains upward momentum and is the only particle of interest involved.

These two points go together, of course. Consider a particle that has a mass of 1. If the negative acceleration of gravity is g, then gravity is reducing this particle’s momentum by 1*g every second. Assuming this particle is at equilibrium and is not changing its height much over time, the particle must be gaining 1*g momentum from some other source. The indirect source is the floor, which presses up on some particles, but the direct source is the individual collisions, which on average supply the particle with 1*g upward momentum.

These observations give us some confidence in the explanation, but one might still be puzzled as to how collisions have an average positive effect if only collisions between particles and the floor can have a net upward change in momentum, and most particles never hit the floor. The answer lies in a mathematical subtlety: the collisions undergone by each individual particle can (on average) increase momentum even if all the individual collisions between particles conserve momentum.

As an example, let’s say we looked at the collisions in a certain window of time and found:

  • Particle A rebounded off the floor, which increased its (upward) momentum by 5.
  • Then particle A, now moving upward, hit particle B, losing 4 units of momentum (which particle B gained).
  • This sent particle B moving upward, where it hit particle C, losing 3 units of momentum, which particle C gained.
  • Similarly, particle C hits particle D, transferring 2 units of momentum, and particle D hits particle E, transferring 1 unit of momentum. Particle E is at the top of the “cloud” of particles, so it does not hit another particle until it begins falling back down.

In this example, each individual collision conserved momentum, yet every particle enjoyed a net gain of (upward) momentum because it gained slightly more momentum in one collision than it lost in the other. This was, of course, a toy example, but it is easy to see that it must be this way because the interaction of the particles must counteract the force of gravity.

Older posts «